数学组 杨兴军
1 问题的提出
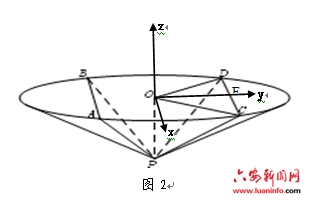
2013安徽高考数学理科第19题如下:
平面PAB, CD 平面PCD,而MN不包含于这两个平面,所以MN∥平面PAB,MN∥平面PCD,所以MN平行于平面PAB与平面PCD的交线;而MN 底面, 底面,所以平面PAB与平面PCD的交线平行于MN,得证.
评注:此法立足于不设(作)出平面PAB与平面PCD的交线,而是充分利用了一道习题的结论:若一条直线与两相交平面都平行,则它与交线平行.考生证明时存在的主要问题是:直接由MN∥AB,MN∥CD推出MN平行于平面PAB与平面PCD的交线,没有中间理由. 实际上,由于其既不是定义、定理,也不是公理、推论、性质,因而在高考中直接运用不太合适.
证法2:设平面PAB 平面PCD ,由AB∥CD,CD 平面PCD,AB 平面PCD,可得AB∥平面PCD;又因为AB 平面PAB,平面PAB 平面PCD ,所以 ∥AB.由AB 底面,而 底面可知, 与底面平行.
评注:此法立足于设出交线,再利用“线线平行”与“线面平行”的相互转化证明结论.考生证明时存在的突出问题是:(1)设(作)出交线 后,即默认 ∥AB∥CD,没有进行证明;(2)运用线面平行的判定定理或性质定理时,条件没有全部列举出来,逻辑不够严密.
证法3:作直线PQ∥AB,由公理2“过不在同一直线上的三点,有且只有一个平面”易得,直线 平面PAB,又∵AB∥CD,∴PQ∥CD,同理有直线 平面PCD,所以直线PQ为平面PAB与平面PCD的交线.而CD底面,PQ 底面,所以PQ∥底面,即平面PAB与平面PCD的交线平行于底面.
评注:此法立足于先保证所作直线与AB、CD都平行,再设法证明所作直线即为两平面的交线.考生证明时存在的主要问题是:默认了所作直线PQ就是平面PAB与平面PCD的交线,根本没有加以证明.
证法4:过点P作平面α∥底面,设平面PAB α=PM,平面PCD α=PN,由面面平行的性质定理得到PM∥AB以及PN∥CD,而AB∥CD,所以根据公理4,PM、PN只能重合(即为平面PAB与平面PCD的交线 ).而AB(CD) 底面, 底面,故 ∥底面.
评注:此法采用了同一法思想,先分别得到两条直线PM、PN,再根据“过直线外一点与已知直线平行的直线具有唯一性”得出直线PM、PN重合,即为两平面的交线.考生证明时存在的主要问题是:对直线PM、PN为什么重合说理不清,敷衍了事.
证法5:设平面PAB 平面PCD .假设 不平行于底面,又 底面(∵P∈ , 底面),则 与底面相交,设交点为Q,则只能有Q∈AB(否则,不共线三点A、B、Q确定唯一平面,从而平面PAB与底面重合,显然矛盾),同理有Q∈CD,这与AB∥CD矛盾,所以假设不成立,即 ∥底面.
评注:此法采用了反证法思想,先假设交线与底面不平行,再设法得出矛盾.考生证明时存在的主要问题是:运用反证法的逻辑顺序混乱,推理时往往只写结论,没有相应的依据,因而矛盾的得出显得牵强附会.
证法6:设CD中点为F,连OF、PF,由圆的性质,有∠COD=2∠COF,OF⊥CD..
因为OP⊥底面,CD 底面,所以OP⊥CD,又OP∩OF=O,故CD⊥平面OPF,又CD 平面PCD,因此平面OPF⊥平面PCD,从而直线OP在平面PCD上的射影为直线PF,故∠OPF为OP与平面PCD所成的角.

设 ,平面PCD的法向量为 ,则由 得 ,因此可取 .不妨设AB、CD在圆心O两侧,设OP与平面PAB所成的角为 ,同理可得平面PAB的法向量 .
设平面PAB与平面PCD的交线 的方向向量 ,则由 即 得 ,所以 ( ),又底面的一个法向量为 ,由 知 ,即 与底面平行.
评注:此法运用了判定线面平行的向量方法:若平面外一条直线的方向向量与该平面的法向量垂直,则直线与平面平行.考生遇到的困难主要有:(1)不知如何建系——图中没有现成的两两垂直且交于一点的三条直线;(2)只建系,不说理——随便建个系不作说明,或建系前不说理;(3)不会写相关点的坐标——对相关点在空间直角坐标系中的位置不习惯,或感到数量关系不够明显;(4)不会求两平面交线的方向向量——受制于平时训练中狭隘的固有模式,对基本知识的理解不深刻、对基本技能的掌握不牢固,无法在短时间内迅速找到求解思路.
(本问还有其它证法,如利用空间解析几何的平面方程知识等,但由于在受访考生的答题中并没有出现,此处从略)
2.2 第(Ⅱ)问的解题分析
解法1:同第(Ⅰ)问证法6可得,∠OPF即为OP与平面PCD所成的角.
设OP=h ,由已知∠OPF=60○ ,得 ;又∠PCD=22.5○,得 ;由 及tan22.5○﹥0得 ,从而
.所以在 中, ,故
.
评注:此为第(Ⅱ)问的基本解法,要求考生能以线面垂直关系为基础,根据线面角的定义正确构图,然后结合三角公式熟练地进行计算.考生出现的问题主要集中在三个方面:一是将题设所给的线面角(60○)误以为是∠OPC (或∠OPD)或没有正确算出22.5○的三角函数值(没有看出22.5○是45○的一半)而导致计算错误或冗长或半途而废;二是能正确指出上述线面角但缺乏必要的文字说明;三是解题方向不明确,不能将数量关系集中到一个三角形中,导致计算凌乱,不得要领.
解法2:同解法1有 , .
设 ,
则由 ,得 ,
由 ,得 ,
又 ,代入可得
.
评注:这是向量方法中的基向量法(区别于向量坐标法),此法没有运用二倍角公式,而是直接将∠COD看做两个向量 、 的夹角,利用向量的数量积计算求解.由于在很多考生心目中,向量法等同于向量坐标法,因此,采用此法的考生极少.
限于篇幅,第(Ⅱ)问的其它解法不再赘述.
3 对立体几何教学的几点思考
从以上解题分析中不难看出,本题的绝度难度并不大,众多解法中无一需要特殊的解题技巧,均为考生常见的通性通法.那么,到底是什么原因造成全省众多考生在这样一道试题上纷纷落马呢?原因只能归结为:广大考生对立体几何的知识、方法、思想的认识、理解和掌握远没有达到本质的程度,解题模式化现象严重,对稍微陌生一些的情境适应性很差(如很多考生虽然对“倒圆锥”感到十分难受,但根本想不到把它“正过来”),逻辑推理能力明显下降更是不争的事实.进而,可以认为我们的立体几何教学很多时候是无效的(虽然作了大量训练,但并没有做到让学生“知其然,更知其所以然”),只是这种无效性在常规的问题情境下没有机会暴露出来而已!或者也可以这样说:“懂而不会现象”在立体几何教学中广泛存在,应引起中学数学教育工作者的深刻反思.
3.1 立体几何的推理证明不能削弱
“直观感知,操作确认”属于“实验几何”范畴,而“推理证明”则属于“论证几何”范畴.作为新课程突出“过程性目标”的重要体现,立体几何教学中强调“直观、操作”是无可厚非的,何况,培养直观能力本身也是几何教学的重要目标.然而,几何教学的关键和最终落脚点应该是逻辑推理证明,不能仅仅停留在空间图形的直观上.应该执行“直观引领,论证‘善后’”的教学导向.
本应通过严格推导才能得出的结论,竟然“看一看,做一做”就认可了,根本不需要理由,学习难度降低了,随之而来的是学生的素质与能力也大大下降.现在高中学生的数学作业,前言不搭后语的逻辑混乱较之于新课标前普遍多了,凡是需要的解题条件,不加严格的推理论证,而通过“看出来的”不在少数,这充分说明立体几何课程中推理证明的弱化已经对其它数学分支的学习产生明显的负面影响.
立体几何的教学,确实要避免过繁过难的问题,但需要精中求简,需要保证立体几何的逻辑体系不致削弱.著名数学特级教师黄安成先生曾于2006年大声呼吁“为‘三垂线定理及其逆定理’正名”,对新教材中取消这两个定理感到痛心疾首;已故的谷超豪先生在2010年接受独家专访时曾说:“好多次听学校教高等数学的老师反映,新进来的不少大学生不会写证明题,不会逻辑演绎.现在数学中几何的推理证明被淡化,不鼓励学生问‘为什么’,不鼓励学生通过逻辑推理来逐步证明自己的结论,数学就失去了它的重要功效之一.”这被华东师范大学的张奠宙、赵小平两位教授称为“谷超豪之忧”.杨乐院士、已故的陈省身先生等著名数学家也对几何教学的现状表达过类似的观点.
3.2 “综合几何”的基础地位不能动摇
自从引入了空间向量,立体几何的学习似乎抓到了一根救命稻草,一夜之间容易了许多.无论是线线、线面、面面等位置关系,还是夹角、距离等数量关系,都可以转化为用向量来解决,并且归结为一系列模式化的解题程序.
的确,向量兼具代数与几何的双重身份,通常可以省略构图的繁琐,在解决立体几何问题时具有独特的优势,如线面垂直判定定理的证明,向量法就比传统的综合几何法简单得多,其它诸如异面直线的距离、二面角等问题,向量法的优势往往更加明显.
然而,凡事都有两面性.向量法在增加运算的同时,也大幅减少了几何推理,久而久之,学生的眼中只有运算求解,没有逻辑证明.教材中的定义、公理、定理、推论、性质等立体几何基础知识,只能成为学生脑海中的模糊记忆,说不清楚、讲不明白,更是用不顺手.
虽然几何并不是唯一培养学生推理能力的载体,但仍然具有不可替代的主要作用,就像“长跑”这一传统的锻炼运动员体能与意志力的训练方法,在科技发达的今天,在训练方法多样化、现代化的今天,“长跑”仍被教练员们在训练中采用,它仍具有其它训练难以代替的功能.
因此,立体几何教学应以综合几何为基础,与向量几何相互配合,“两条腿走路”,既能真正落实几何教学的主要目标——培养学生的空间想象能力和逻辑推理能力,又能使一些繁难的几何问题得到有效解决.
3.3 几何教学的客观规律不能违背
立体几何的教学,有着自己独有的客观规律,教师的教学行为是否遵循了如下规律,对学生学习的有效性(有效率、有效果、有效益)起着举足轻重的影响.
(1)充分利用模型.要始终如一地发挥模型在立体几何学习中的作用,培养学生丰富的立体感,让学生感受空间图形是各种实物的进一步抽象,增强空间图形真实感,为空间想象能力的提升奠定基础,这里的模型既包括可以购买的现成的标准模型,也包括教师为克服教学难点而自制的模型或多媒体视频中的动画,还包括学生身边的实物等. 事实上,很多学生的空间想象能力的培养没有落到实处,其根本原因就是缺乏模型意识.
(2)强化主体参与.任何教学都要注重主体参与,立体几何教学尤应如此.有人把直观基础上的推理论证比作几何的“灵魂”,把需要添加的辅助线比作几何的“血脉”,人的灵魂需要自己感悟,人的血脉需要自身创造,立体几何的学习同样如此.新知教学中,一个结论的形成,需要学生在教师引导下进行充分的、主动的合作探究;解题教学中,一种思路的获得,更需要学生在积极参与中迸发出思维的火花,需要频现学生兴趣盎然地讨论一道题证法的盛景.
(3)注重语言训练.立体几何富含各种数学语言:文字语言、图形语言、符号语言等,每种语言代表学生的一种认识和理解,在不同语言之间转换能反映出学生对知识理解的不同方面,能培养学生对知识的多元联系能力,能更好揭示知识的本质.应在充分发挥教师自身示范作用的基础上,强化对学生语言逻辑性、严谨性、条理性、简洁性等方面的规范训练,力求杜绝“有想法讲不出”、“讲得出写不出”、“能写出但没依据”、“有依据但写不准”等现象的发生.
(祝志好老师编审)
